84. 柱状图中最大的矩形

发表评论
380 views

 ›
84. 柱状图中最大的矩形

官方链接

https://leetcode-cn.com/problems/largest-rectangle-in-histogram

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

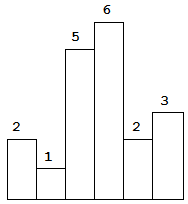
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

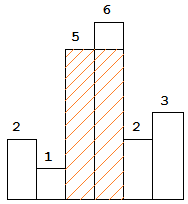
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 

示例:

输入: [2,1,5,6,2,3]
输出: 10

解法一(暴力1)：

注意 这里 i, j 可以重合

for i->1, i->n-1
  for j->i,  j->n-1
    (i,j) -> 最小高度， area
    update max-area
class Solution {
    public int largestRectangleArea(int[] heights) {
        // if (heights.length == 0) return 0;
        // if (heights.length == 1) return heights[0];
        int area = 0;
        for (int i = 0; i < heights.length; i++) {
            for (int j = i; j < heights.length; j++) {
                int minHeight = Integer.MAX_VALUE;
                for(int k = i; k <= j; k++) {
                    minHeight = Math.min(minHeight, heights[k]);
                }
                area = Math.max(area, (j - i + 1) * minHeight);
            }
        }
        return area;
    }
}

解法二(暴力2)：

for i ->0, n-1
  找到 left bound， right bound
  area = heigh[i] * (right -left)
  update max-area
class Solution {
    public int largestRectangleArea(int[] heights) {
        int area = 0;
        for (int i = 0; i < heights.length; i++) {
            int height = heights[i];
            int leftBound = i;
            int rightBound = i;

            for(int j = i; j >= 0; j--) {
               if (height > heights[j]) {
                   break;
               } else {
                   leftBound = j;
               }
            }

            for (int k = i; k < heights.length; k++) {
               if (height > heights[k]) {
                   break;
               } else {
                   rightBound = k;
               }
            }
            area = Math.max(area, (rightBound - leftBound + 1) * height);
        }
        return area;
    }
}

解法三

单调栈 stack

class Solution {
    public int largestRectangleArea(int[] heights) {

        Stack<Integer> stack = new Stack<>();
        stack.push(-1);
        int maxarea = 0;

        for (int i = 0; i < heights.length; i++) {
           while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
               maxarea = Math.max(maxarea, heights[stack.pop()] * (i - stack.peek() - 1));
           }
           stack.push(i);
        }

        while(stack.peek() != -1) {
            maxarea = Math.max(maxarea, heights[stack.pop()] * (heights.length - stack.peek() - 1));
        }

        return maxarea;
    }
}

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
      heights = [0] + heights + [0]
      stack = []
      res = 0
      for i in range(len(heights)):
        while stack and heights[stack[-1]] > heights[i]:
          tmp = stack.pop()
          res = max(res, (i-stack[-1]-1) * heights[tmp])
        stack.append(i)
      return res