52. N皇后 II

发表评论
308 views

 ›
52. N皇后 II

官方链接

https://leetcode-cn.com/problems/n-queens-ii/

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

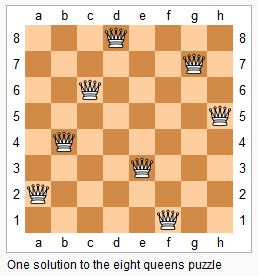
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

提示：

皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是"吃子"。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一或七步，可进可退。（引用自 百度百科 - 皇后 ）

解法一

位运算

class Solution {
    private int count = 0;
    public int totalNQueens(int n) {
        dfs(n, 0, 0, 0, 0);
        return count;
    }

    private void dfs(int n, int row, int col, int pie, int na) {
        // recursion terminator
        if (row >=n) {
            count++;
            return;
        }
        int bits = (~(col|pie|na)) & ((1 << n) -1); // 我们只关心最后的 n 位, 这一步是得到最后 n 位中的有效的空位
        while (bits > 0) {
            int p = bits & (-bits); // 得到 最后一位的 1, 用来放 queen
            dfs(n, row + 1, col | p, (pie | p) << 1, (na | p) >> 1);
            bits &= bits - 1; // 去掉最后一个 1
        }
    }
}

class Solution {
    private int size;
    private int count;

    private void solve(int row, int ld, int rd) {
        if (row == size) {
            count++;
            return;
        }
        int pos = size & (~(row | ld | rd));
        while (pos != 0) {
            int p = pos & (-pos);
            pos -= p; // pos &= pos - 1;
            solve(row | p, (ld | p) << 1, (rd | p) >> 1);
        }
    }

    public int totalNQueens(int n) {
        count = 0;
        size = (1 << n) - 1;
        solve(0, 0, 0);
        return count;
    }
}

class Solution:
    def totalNQueens(self, n): 
        if n < 1: return [] 
        self.count = 0 
        self.DFS(n, 0, 0, 0, 0) 
        return self.count

    def DFS(self, n, row, cols, pie, na): 
        # recursion terminator 
        if row >= n: 
            self.count += 1 
            return

        bits = (~(cols | pie | na)) & ((1 << n) - 1)  # 得到当前所有的空位

        while bits: 
            p = bits & -bits # 取到最低位的1
            bits = bits & (bits - 1) # 表示在p位置上放入皇后
            self.DFS(n, row + 1, cols | p, (pie | p) << 1, (na | p) >> 1) 
            # 不需要revert  cols, pie, na 的状态

class Solution {
public:
    int totalNQueens(int n) {

        dfs(n, 0, 0, 0, 0);
        return this->res;
    }

    void dfs(int n, int row, int col, int ld, int rd) {
        if (row >= n) { res++; return; }

        // 将所有能放置 Q 的位置由 0 变成 1，以便进行后续的位遍历
        int bits = ~(col | ld | rd) & ((1 << n) - 1);
        while (bits > 0) {
            int pick = bits & -bits; // 注: x & -x
            dfs(n, row + 1, col | pick, (ld | pick) << 1, (rd | pick) >> 1);
            bits &= bits - 1; // 注: x & (x - 1)
        }
    }


private:
    int res = 0;
};