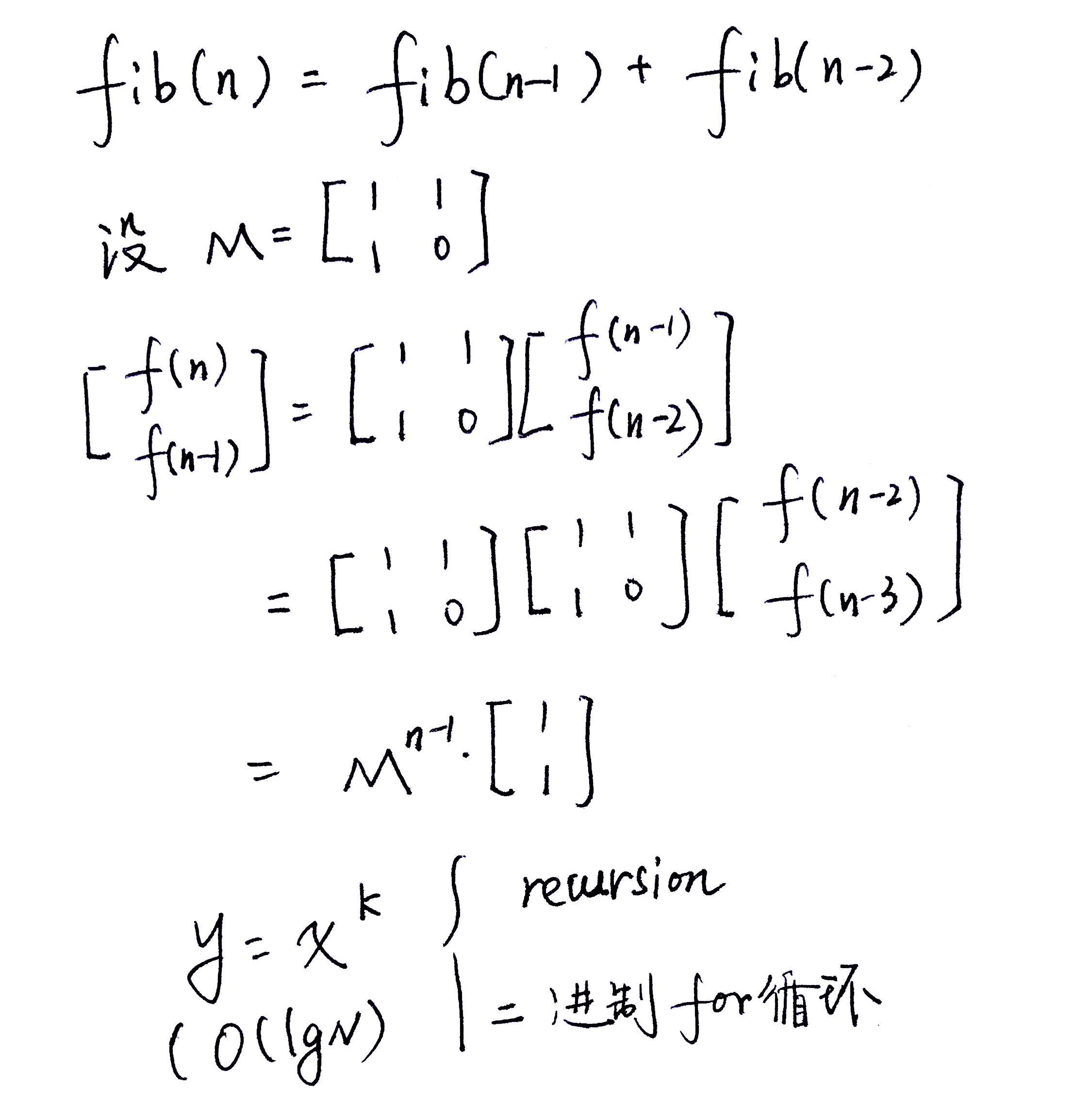官方链接
https://leetcode-cn.com/problems/climbing-stairs
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶思路
单词:
Elevator 电梯
Escalator 扶梯相邻两步的步伐不能相同
1: 1
2: 2
3: f(1) + f(2) mutual exclusive, conmplete exhaustive
4: f(3) + f(2)
f(n) = f(n-1) + f(n-2) : Fibonacci
暴力解法时间复杂度为 O(2^n) (画出状态树,第一层一个,第二层两个,第三层四个..., 为指数级)
解法一 记忆化搜索
O(n)
class Solution {
Map<Integer, Integer> mem = new HashMap<>();
public int climbStairs(int n) {
if (n <= 2) return n;
if (mem.containsKey(n)) return mem.get(n);
mem.put(n, climbStairs(n - 1) + climbStairs(n - 2));
return mem.get(n);
}
}
解法二 DP
class Solution {
public int climbStairs(int n) {
if (n <= 2) return n;
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i -2];
}
return dp[n];
}
}
DP 只存储最后两个元素
class Solution {
public int climbStairs(int n) {
if (n <= 2) return n;
int[] dp = new int[3];
dp[0] = 1;
dp[1] = 2;
int result = 0;
for (int i = 3; i <= n; i++) {
dp[2] = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = dp[2];
}
return dp[2];
}
}
DP 简化
class Solution {
public int climbStairs(int n) {
if (n <= 2) return n;
int f1 = 1, f2 = 2, f3 = 0;
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}
}
class Solution:
def climbStairs(self, n: int) -> int:
x, y = 1, 1
for _ in range(1, n):
x, y = y, x + y
return y
解法三
转换为零钱兑换问题
每次可以用 1 块钱, 2 块钱,凑 n 元。
爬楼梯问题变种
每次只能走 1、2、3
class Solution {
public int climbStairs(int n) {
if (n <= 1) return n;
int[] dp = new int[n];
dp[0] = 1;
dp[1] = 2;
dp[2] = 3;
for(int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
return dp[n - 1];
}
}
每次只能走 int[] x = [X1, X2, ..., Xm] 步中的一种
class Solution {
public int climbStairs(int n) {
if (n <= 1) return n;
int[] dp = new int[n];
dp[0] = 1;
dp[1] = 2;
for(int i = 2; i <= n; i++) {
for (int j = 0; j < m; j++) {
dp[i] += dp[i - x[j]]; // 走了 x[j] 步, 必须是从 i - x[j] 上来的
}
}
return dp[n - 1];
}
}
每次只能走 int[] x = [X1, X2, ..., Xm] 步中的一种,且前后不能走相同的步伐
class Solution {
public int climbStairs(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1][x.length];
// dp[i][x[k]] i 表示上到第几阶台阶,第二维表示我走的是几步
dp[0][0] = 1;
dp[1][] = 2;
for(int i = 3; i <= n; i++) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < m; k++) {
if (k != j) dp[i][x[k]] += dp[i - x[j]][x[k]];
}
}
}
int result = 0;
for (int k = 0; k < m; k++) {
result += dp[n][x[k]];
}
return result;
}
}
扩展题
https://leetcode-cn.com/problems/min-cost-climbing-stairs/
矩阵法解决 fibnacii