定义
https://en.wikipedia.org/wiki/Dynamic_programming
https://zh.wikipedia.org/wiki/动态规划
- "Simplifying a complicated problem by breaking it down into simpler subproblems"(in a recursive manager)
- Divide & Conquer + Optimal substructure (分治+最优子结构)
DP 顺推模板
function DP():
dp = [][] # 二维情况
for i = 0 .. M { for j = 0 .. N {
dp[i][j] = _Function(dp[i’][j’]...) }
}
return dp[M][N];关键点
动态规划和递归或者分治 没有根本上的区别 (关键看有无最优的子结构)
共性: 找到重复子问题
差异性: 最优子结构、中途可以淘汰次优解
自底向上
转化递归为 递推
动态规划关键点
- 最优子结构 opt[n] = best_of(opt[n-1]+ opt[n-2], ...)
- 存储中间状态 opt[i]
递推公式 (状态转移方程或者 DP方程)
fib: opt[i] = opt[n-1]+opt[n-2] 二维路径: opt[i,j] = opt[i+1][j]+opt[i][j+1] (且判断 a[i,j] 是否是空地)
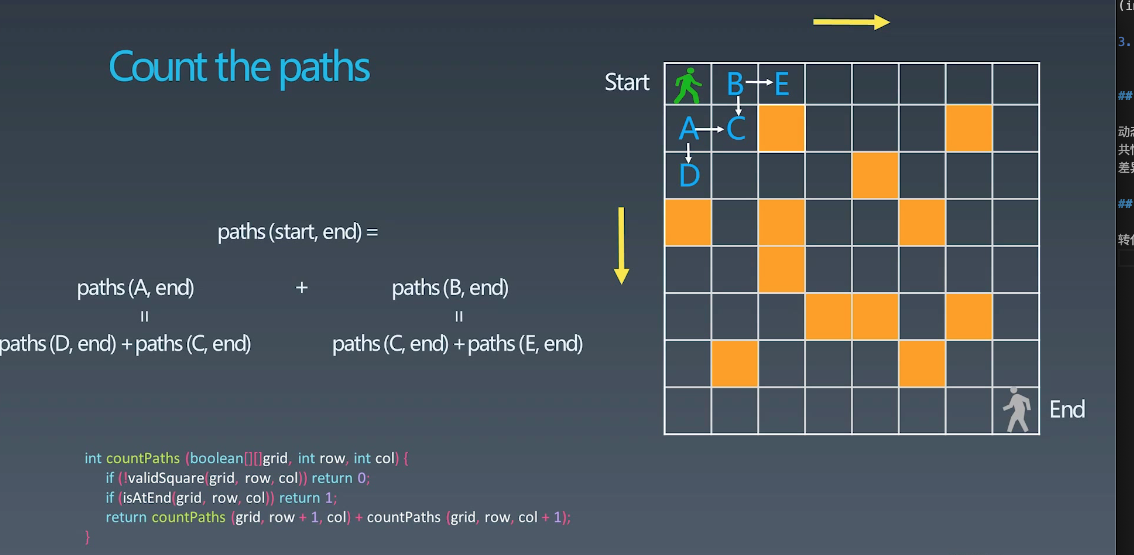
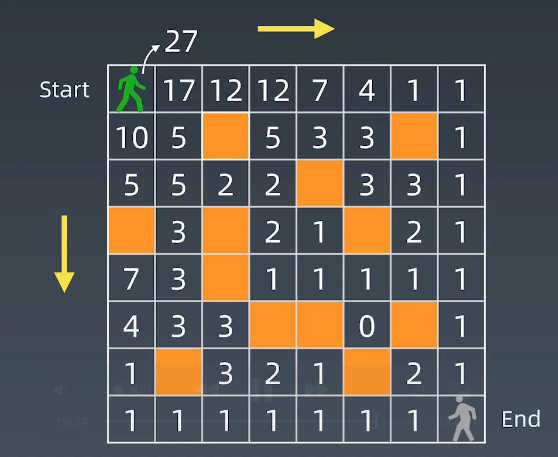
感触
- 人肉递归低效、很累
- 找到最近最简方法,将其拆解成可重复解决的问题
- 数学归纳法思维(抵制人肉递归的诱惑)
动态规划小结
- 打破自己的思维惯性,形成机器思维
- 理解复杂逻辑的关键
- 也是职业进阶的要点要领
3 步 DP
问题抽象化,定义成状态,套用模版,写出嵌套循环,写DP方程
- 子问题
- 状态空间
- DP 方程
MIT 5 步 DP
- 定义子问题
- 猜递推方程
- 合并子问题的解
- 递归 & 记忆化搜索 or 建立 DP 状态表(DP table) 自底向上递推
- 得到原问题的解
leetcode
62.不同路径
63.不同路径 II
70. 爬楼梯
1143.最长公共子序列
120. 三角形最小路径和
53. 最大子序和