并查集 Disjoint Set

发表评论
517 views

 ›
并查集 Disjoint Set

并查集 Disjoint Set

并查集(union & find) 是一种树形结构，用于处理一些不交集(Disjoint Sets) 的合并及查询问题
Find: 确定元素属于哪一个子集。他可以被用来确定两个元素是否属于同一个子集。
Union: 将两个子集合合并成同一个集合

适用场景

  • 组团、配对问题
  • Group or not ?

伪代码

  • makeSet(s):建立一个新的并查集，其中包含 s 个单元素集合。
  • unionSet(x, y):把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。
  • find(x):找到元素 x 所在的集合的代表，该操作也可以用于判断两个元 素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。
def makeSet(x):
    x.parent := x

def Find(x):
    if x.parent == x
        return x
    else:
        return Find(x.parent)

def Union(x, y):
    xRoot := Find(x)
    yRoot := Find(y)
    xRoot.parent := yRoot

优化

  • 优化 1: union by rank
def makeSet(x):
    x.parent = x

def Find(x):
    if x.parent == x
        return x
    else:
        return Find(x.parent)

def Union(x, y):
    xRoot := Find(x)
    yRoot := Find(y)

    if xRoot.rank < yRoot.rank:
        xRoot.parent = yRoot
    else if XRoot.rank > yRoot.rank:
        yRoot.parent = xRoot
    else:
        yRoot.parent = xRoot
        xRoot.rank = xRoot.rank + 1
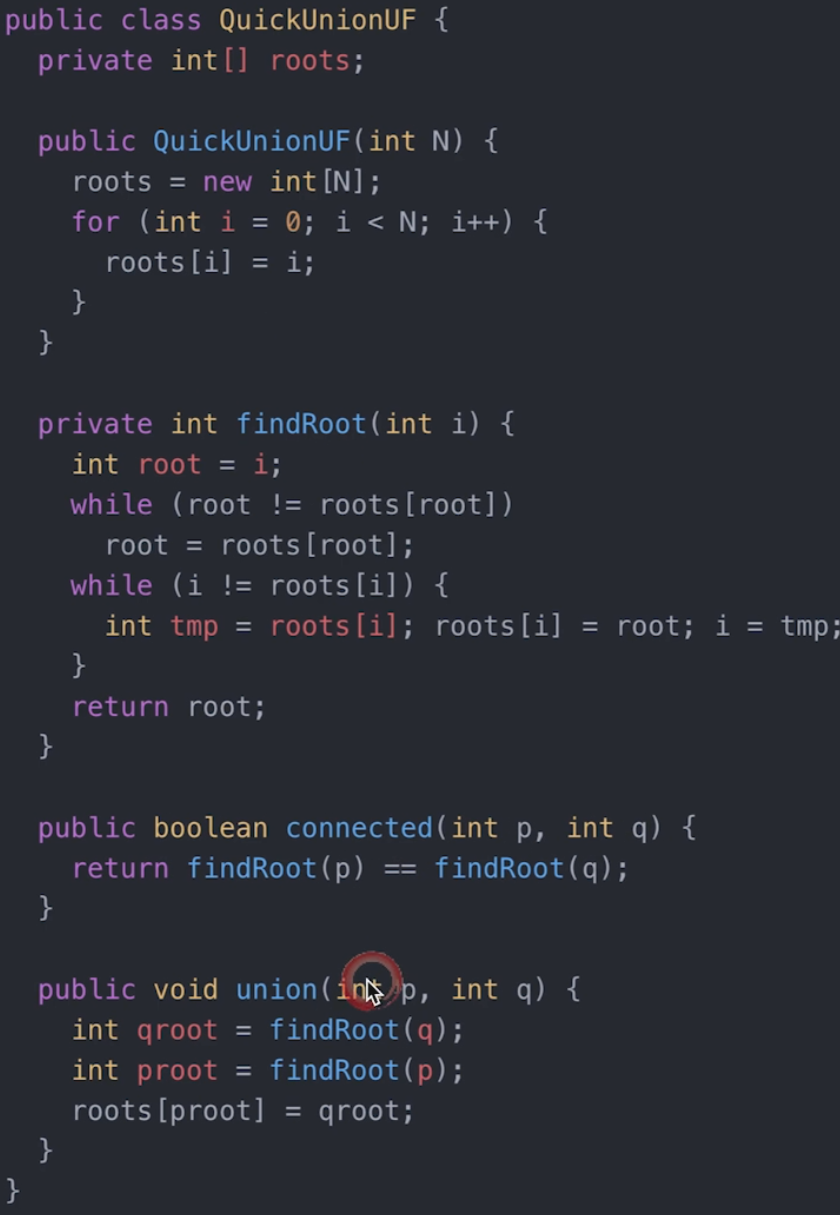
  • 优化2: 调用 find(d) 时路径压缩
class UnionFind {
    private int count = 0;
    private int[] parent;

    public UnionFind(int n) {
        count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    public int find(int p) {
        while (p != parent[p]) {
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;
    }

    // 路径压缩
    public int findRoot(int i) {
        int root = i;
        while (root != parent[root]) {
            root = parent[root];
        }
        while (i != parent[i]) {
            int tmp = parent[i];
            parent[i] = root;
            i = tmp;
        }
        return root;
    }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;
        parent[rootP] = rootQ;
        count--;
    }
}

def init(p):
# for i=0 ..n:p[i]=i;
p=[i for i in range(n)]
def union(self,p,i,j):
    p1=self.parent(p,i)
    p2=self.parent(p,j)
    p[p1]=p2

def parent(self,p,i):
    root=i
    while p[root]!=root:
        root=p[root]
    while p[i]!=i: # 路径压缩
        x=i;i=p[i];p[x]=root
    return root

class UnionFind(object):
    def __init__(self, grid):
        m, n = len(grid), len(grid[0])
        self.count = 0
        self.parent = [-1] * (m * n)
        self.rank = [0] * (m * n)
        for i in range(m):
            for j in range(n):
                if grid[i][j] == '1':
                    self.parent[i * n + j] = i * n + j
                    self.count += 1

    def find(self, i):
        if self.parent[i] != i:
            self.parent[i] = self.find(self.parent[i])
        return self.parent[i]

    def union(self, x, y):
        rootx = self.find(x)
        rooty = self.find(y)

        if rootx != rooty:
            if self.rank[rootx] > self.rank[rooty]:
                self.parent[rooty] = rootx
            elif self.rank[rootx] < self.rank[rooty]:
                self.parent[rootx] = rooty
            else:
                self.parent[rooty] = rootx
                self.rank[rootx] += 1
            self.count -= 1