树

二叉树

完全二叉树

用数组存储

常见平衡二叉树

二三树
AVL
红黑树
B 树
B+
⭐️slpay 伸展树
⭐️treap

问题

树的面试题一般都是递归的，这是为什么？

可视化 DEMO

树的遍历
二叉搜索树 demo

树和图的差别

看是否有环，有环为图

平衡树

https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

二叉搜索树 Binary Search Tree

二叉搜索树，也称为二叉搜索排序树、有序二叉树(Ordered Binary Tree)、排序二叉树(Sorted Binary Tree), 是指一棵空树 或者具有下列性质的二叉树：

1. 左子树上 所有节点 的值均小于它的根节点的值
2. 右子树上 所有节点 的值均大于它的根节点的值
3. 依次类推：左、右子树也分别为二叉查找树(这就是 重复性！)

中序遍历：升序排列

二叉搜索树 查询操作时间复杂度 O(logn)

AVL 树

1. 发明者 G. M. Adelson-Velsky 和 Evgenii Landis
2. Balance Factor(平衡因子): 是它的左子树的高度减去它的右子树的高度(有时相反)。 balance factor = {-1, 0, 1}
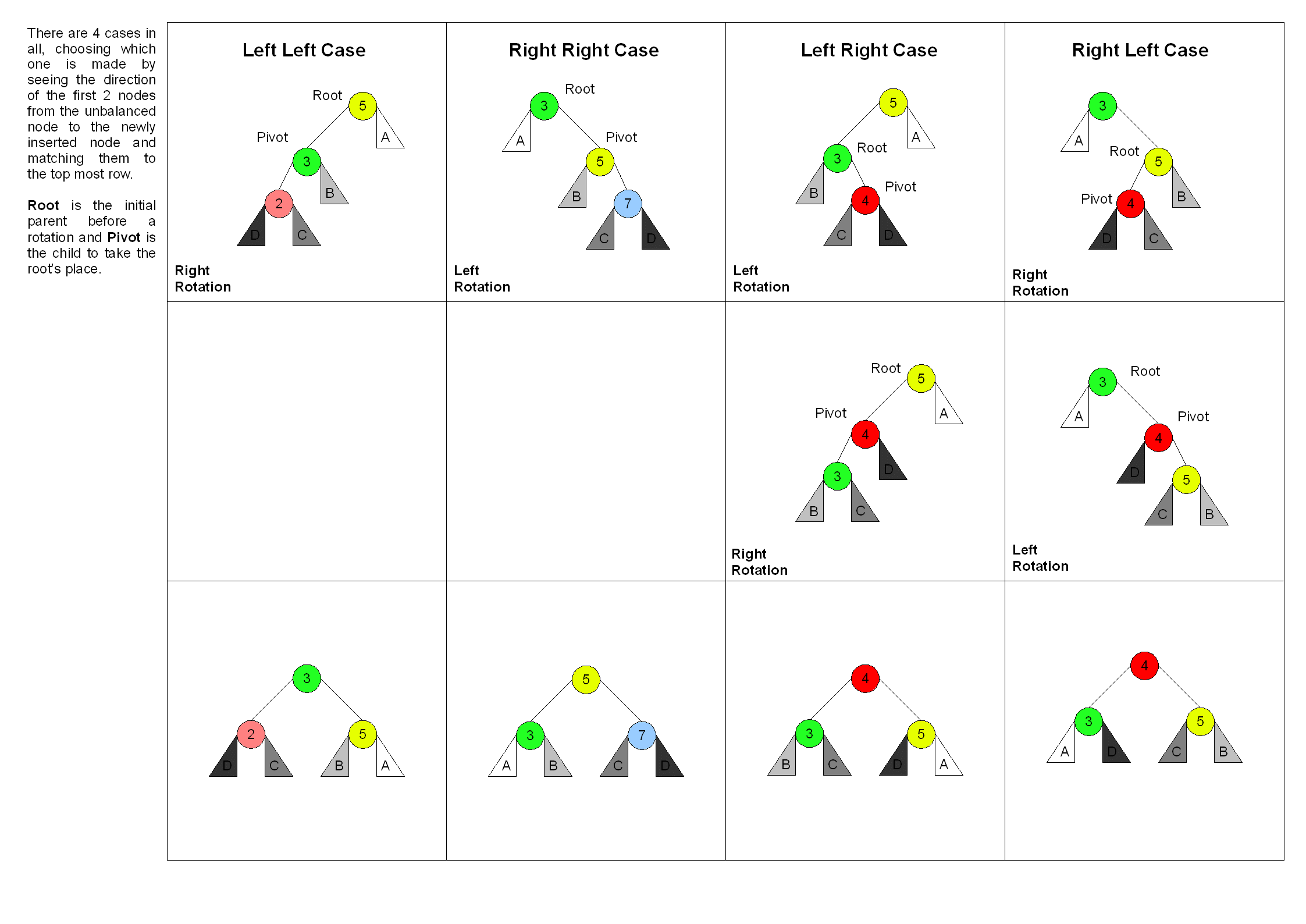
3. 通过旋转操作来进行平衡(四种)
4. 平衡二叉树

AVL 树旋转操作

1. 左旋
2. 右旋
3. 左右旋
4. 右左旋

https://en.wikipedia.org/wiki/Tree_rotation#/media/File:Tree_Rebalancing.gif

AVL 总结

1. 平衡二叉搜索树
2. 每个结点存 balance factor = {-1, 0, 1} 3. 四种旋转操作
   不足:结点需要存储额外信息、且调整次数频繁

红黑树

Red-black Tree 红黑树是一种 近似平衡 的二叉搜索树(Binary Search Tree)，它能够确保任何一个结点的左右子树的 高度差小于两倍。具体来说，红黑树是满足如下条件的二叉搜索树:

• 每个结点要么是红色，要么是黑色
• 根节点是黑色
• 每个叶节点(NIL节点，空节点)是黑色的
• 不能有相邻接的两个红色节点
• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

关键性质

从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

对比

• AVL trees provide faster lookups than Red Black Trees because they are more strictly balanced.

• Red Black Trees provide faster insertion and removal operations than AVL trees as fewer rotations are done due to relatively relaxed balancing.

• AVL trees store balance factors or heights with each node, thus requires storage for an integer per node whereas Red Black Tree requires only 1 bit of information per node.

• Red Black Trees are used in most of the language libraries like map, multimap, multisetin C++ whereas AVL trees are used in databases where faster retrievals are required.

示例代码

Python

class TreeNode:
  def __init__(self, val):
    self.val = val
    self.left, self.right = None, None

C++

struct TreeNode {
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode (int x): val(x), left(NULL), right(NULL) {}
}

Java

public int val;
  public TreeNode left, right;
  public TreeNode (int val) {
    this.val = val;
    this.left = null;
    this.right = null
  }

二叉树的遍历

1.前序(Pre-order): 根-左-右 2.中序(In-order): 左-根-右 3.后序(Post-order): 左-右-根

遍历示例代码

def preorder(self, root):
  if root:
    self.traverse_path.append(root.val)
    self.preorder(root.left)
    self.preOrder(root.right)

def inorder(self, root):
  if root:
    self.inorder(root.left)
    self.traverse_path.append(root.val)
    self.inorder(root.right)

def postorder(self, root):
  if root:
    self.postorder(root.left)
    self.postorder(root.right)
    self.traverse_path(root.val)