- 单链表

每个节点只包含一个指针,即后继指针
头节点指向整条链表,尾节点的后继指针指向空地址 null
插入和删除节点的时间复杂度为O(1),查找的时间复杂度为O(n)
- 双向链表
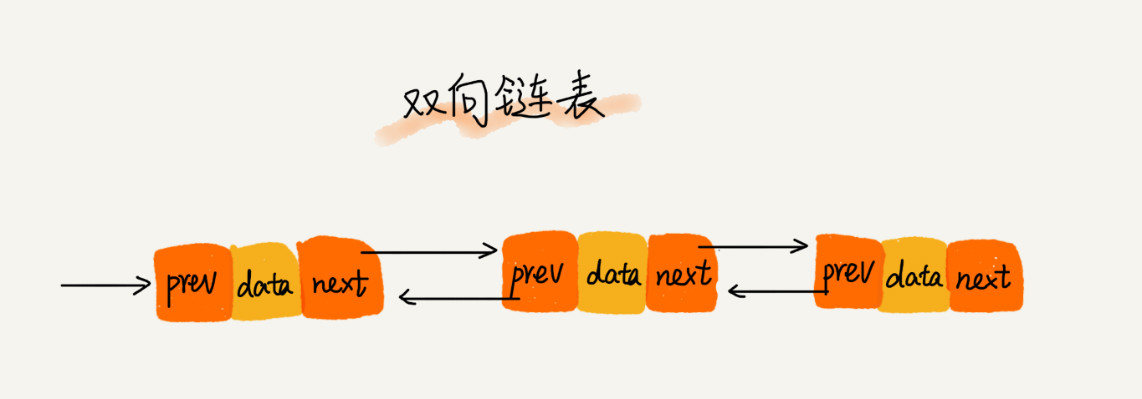
节点除了存储数据外,还有两个指针分别指向前一个节点地址(前驱指针prev)和下一个节点地址(后继指针next)
头节点的前驱指针prev和尾节点的后继指针均指向空地址
- 循环链表
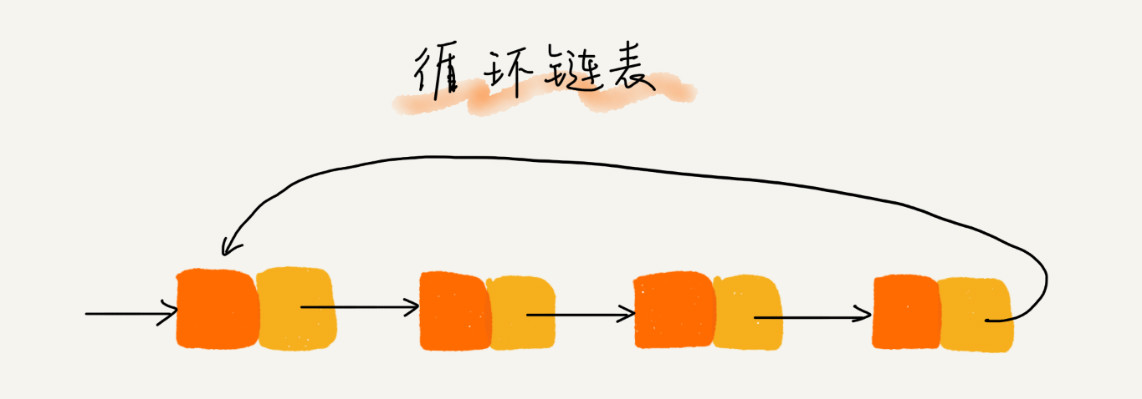
除了尾节点的后继指针指向头节点的地址外均与单链表一致。 适用于存储有循环特点的数据,比如 约瑟夫斯问题
- 双向循环链表
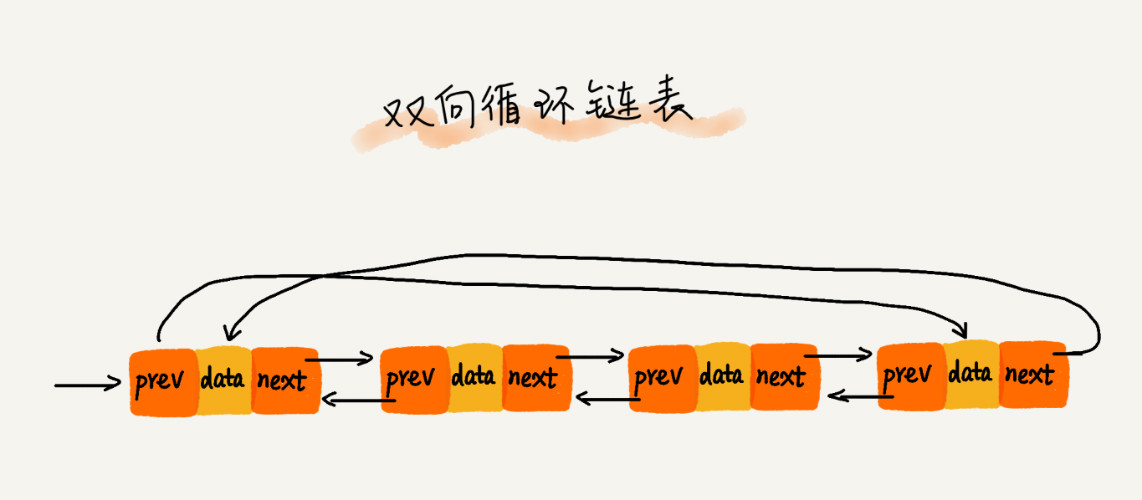
头节点的前驱指针指向尾节点,尾节点的后继指针指向头节点
链表的时间复杂度
| 操作 | 复杂度 |
|---|---|
| space | O(n) |
| 查找 lookup | O(n) |
| 插入 insert prepend | O(1) |
| 插入 insert append | O(1) |
| 删除 delete | O(1) |
数组和链表的对比
| 时间复杂度 | 数组 | 链表 |
|---|---|---|
| 插入删除 | O(n) | O(1) |
| 随机访问 | O(1) | O(n) |
插入删除较多,用链表
数组在实现上使用连续的内存空间,可以借助CPU的缓冲机制预读数组中的数据,访问效率更高
链表在内存中并不是连续存储,所以对CPU缓存不友好,没办法预读
Java 中的 双向链表:
LinkedHashMap
缓存淘汰策略
- 先进先出策略FIFO(First In,First Out)
- 最少使用策略LFU(Least Frequently Used)
- 最近最少使用策略LRU(Least Recently Used)
LRU:活在当下。比如在公司中,一个新员工做出新业绩,马上会得到重用
LFU:以史为镜。还是比如在公司中,新员工必须做出比那些功勋卓著的老员工更多更好的业绩才可以受到老板重视,这样的方式比较尊重“前辈”
基于链表实现LRU缓存淘汰算法
我们维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
1.如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
2.如果此数据没有在缓存链表中,又可以分为两种情况:
如果此时缓存未满,则将此结点直接插入到链表的头部;
如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
这样我们就用链表实现了一个LRU缓存
问题
如果字符串是通过单链表来存储的,那该如何来判断是一个回文串呢?你有什么好的解决思路呢?相应的时间空间复杂度又是多少呢
由于回文串最重要的就是对称,那么最重要的问题就是找到那个中心,用快指针每步两格走,当他到达链表末端的时候,慢指针刚好到达中心,慢指针在过来的这趟路上还做了一件事,他把走过的节点反向了,在中心点再开辟一个新的指针用于往回走,而慢指针继续向前,当慢指针扫完整个链表,就可以判断这是回文串,否则就提前退出,总的来说时间复杂度按慢指针遍历一遍来算是O(n),空间复杂度因为只开辟了3个额外的辅助,所以是o(1) 时间复杂度O(n), 空间复杂度O(1)
链表的四个边界条件
- 如果链表为空时
- 如果链表只包含一个节点时
- 如果链表只包含两个节点时
- 代码逻辑在处理头尾节点时
利用 "哨兵" 简化实现难度
介绍
如果我们引入“哨兵”节点,则不管链表是否为空,head指针都会指向这个“哨兵”节点
如果我们引入哨兵结点,在任何时候,不管链表是不是空,head指针都会一直指向这个哨兵结点
我们也把这种有哨兵结点的链表叫带头链表。相反,没有哨兵结点的链表就叫作不带头链表
哨兵结点不存储数据,因为哨兵结点一直存在,所以插入第一个结点和插入其他结点,删除最后一个结点和删除其他结点,都可以统一为相同的代码实现逻辑
未引入哨兵的情况
如果在p节点后插入一个节点,只需2行代码即可搞定:
new_node—>next = p—>next;
p—>next = new_node;
但,若向空链表中插入一个节点,则代码如下:
if(head == null){
head = new_node;
}
如果要删除节点p的后继节点:
p—>next = p—>next—>next;
若是删除链表的最有一个节点(链表中只剩下这个节点):
if(head—>next == null){
head = null;
}
跳跃表
http://redisbook.com/preview/skiplist/content.html
https://www.zhihu.com/question/20202931
练习题
206.单链表反转
141.链表中环的检测
21.两个有序的链表合并
19.删除链表倒数第n个结点
876.求链表的中间结点