时间与空间复杂度

发表评论
587 views

 ›
时间与空间复杂度

时间与空间复杂度

复杂度描述的是算法执行时间（或占用空间）与数据规模的增长关系
和性能测试相比，复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点
复杂度量级，我们可以粗略地分为两类，多项式量级 和 非多项式量级。其中，非多项式量级只有两个：O(2n)和O(n!)
我们把时间复杂度为非多项式量级的算法问题叫作NP（Non-Deterministic Polynomial，非确定多项式）问题
当数据规模n越来越大时，非多项式量级算法的执行时间会急剧增加，求解问题的执行时间会无限增长。所以，非多项式时间复杂度的算法其实是非常低效的算法

Big O notation(大O表示法)

算法的执行时间与每行代码的执行次数成正比，用T(n) = O(f(n))表示，其中T(n)表示算法执行总时间，f(n)表示每行代码执行总次数，而n往往表示数据的规模。 以时间复杂度为例，由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势，所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响，所以在做时间复杂度分析时忽略这些项

O(1): Constant Complexity 常数复杂度
O(log n): Logarithmic Complexity 对数复杂度
O(n): Linear Complexity 线性时间复杂度
O(n^2): N square Complexity 平方
O(n^3): N square Complexity 立方
O(2^n): Exponential Growth 指数
O(n!): Factorial 阶乘

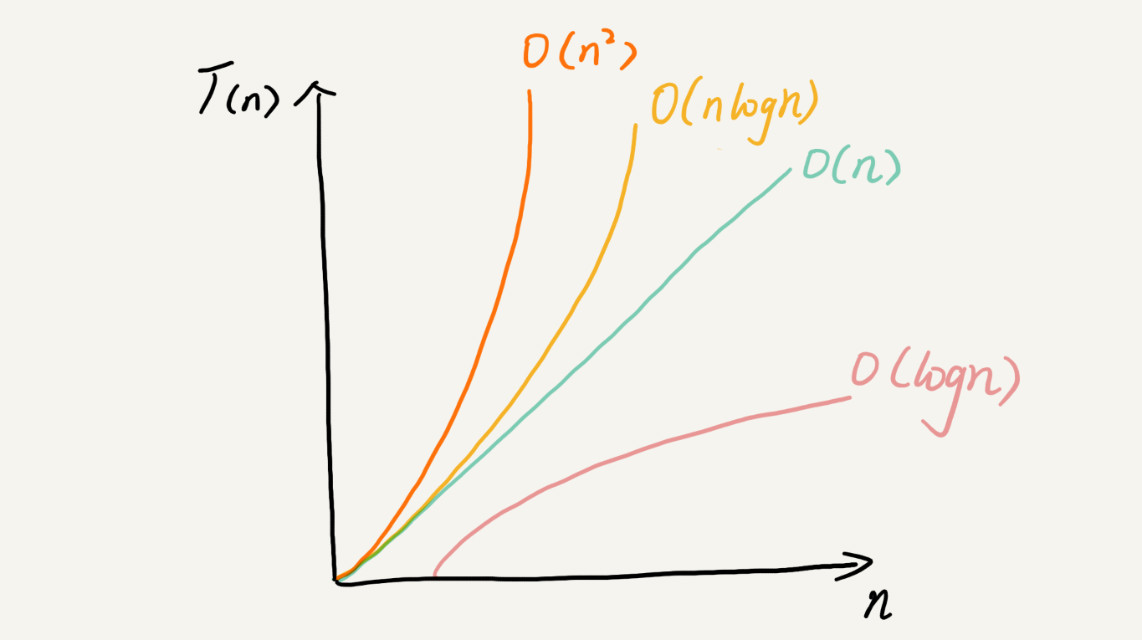
注意： 只看复杂度最高的运算

bigocheatsheet

复杂度分析法则

单段代码看高频：比如循环
多段代码取最大：比如一段代码中有单循环和多重循环，那么取多重循环的复杂度
嵌套代码求乘积：比如递归、多重循环等
多个规模求加法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相加

常用的复杂度级别

多项式阶：随着数据规模的增长，算法的执行时间和空间占用，按照多项式的比例增长。包括，

O(1)（常数阶）、O(logn)（对数阶）、O(n)（线性阶）、O(nlogn)（线性对数阶）、O(n^2)（平方阶）、O(n^3)（立方阶）

非多项式阶：随着数据规模的增长，算法的执行时间和空间占用暴增，这类算法性能极差。包括

O(2^n)（指数阶）、O(n!)（阶乘阶）

如何理解算法时间复杂度的表示法

https://www.zhihu.com/question/21387264

主定理(通过递归来推断时间复杂度)

Master theorem
主定理

算法 复杂度
二分查找 O(log n)
二叉树遍历、深度优先、广度优先、搜索 O(n)
二维有序矩阵排序 O(n) 一维 O(log n)
快排/归并 O(nlog n)

示例

  • 二叉树 前序，中序， 后序遍历的时间复杂度？

    O(n) 因为每节点访问且仅访问一次

  • 图的遍历时间复杂度?

    O(n)

  • 搜索算法 DFS，BFS 的时间复杂度？

    O(n) n 为搜索空间中的节点总数

  • 二分查找的时间复杂度

    时间复杂度 O(log n)

Fibonacci number

写代码要利用缓存或者直接用循环，不要直接用递归

最好、最坏、平均、均摊时间复杂度

  • 最好情况时间复杂度（best case time complexity）

最理想情况下执行的时间复杂度

  • 最坏情况时间复杂度（worst case time complexity）

最坏情况下执行的时间复杂度

  • 平均情况时间复杂度（average case time complexity）

平均时间复杂度的全称 叫 加权平均时间复杂度 或者 期望时间复杂度
所有情况下执行的次数的加权平均值表示

  • 均摊时间复杂度（amortized time complexity）

绝大多数情况下是低级别的复杂度, 个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上
针对这种特殊的场景，引入一种更加简单的分析方法：摊还分析法，通过摊还分析得到的时间复杂度叫均摊时间复杂度
均摊时间复杂度一般都等于最好情况时间复杂度

常见时间复杂度

O(1)

int n = 1000;
System.out.println("Hey - your input is: " + n);

int n = 1000;
System.out.println("Hey - your input is: " + n); System.out.println("Hmm.. I'm doing more stuff with: " + n); System.out.println("And more: " + n);

O(N)

for (int = 1; i<=n; i++) {
  System.out.println("Hey - I'm busy looking at: " + i);
}

O(N^2)

for (int i = 1; i <= n; i++) { 
  for (int j = 1; j <=n; j++) {
    System.out.println("Hey - I'm busy looking at: " + i + " and " + j); 
  }
}

O(log(n))

for (int i = 1; i < n; i = i*2) {
  System.out.println("Hey- I'm busy looking at:" + i);
}

O(k^n)

int fib(int n) {
  if (n <= 2) return n;
  return fib(n-1) + fib(n-2);
}

O(N!)

for (int i = 1; i <= factorial(n); i++){ 
  System.out.println("Hey - I'm busy looking at: " + i);
}