69. x 的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。解法一
二分查找
class Solution {
public int mySqrt(int x) {
int left = 0;
int right = x;
int ans = -1;
while(left <= right) {
int mid = (left+right) >>> 1;
if ((long)mid * mid <= x) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
}
class Solution {
public int mySqrt(int x) {
if (x == 0 | x == 1) return x;
long left = 1, right = x;
while (left <= right) {
long mid = (left + right) >>> 1;
if (mid * mid > x) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return (int)right;
}
}
class Solution {
public int mySqrt(int x) {
if (x == 0 || x == 1) return x;
int left = 0, right = x, result = 0;
while (left <= right) {
int mid = (left + right) >>> 1;
if (mid == x / mid) return mid; // mid * mid 可能会越界,所以直接用除法
else if (mid > x / mid) {
right = mid - 1;
} else {
left = mid + 1;
result = mid;
}
}
return result;
}
}
解法二
牛顿迭代法

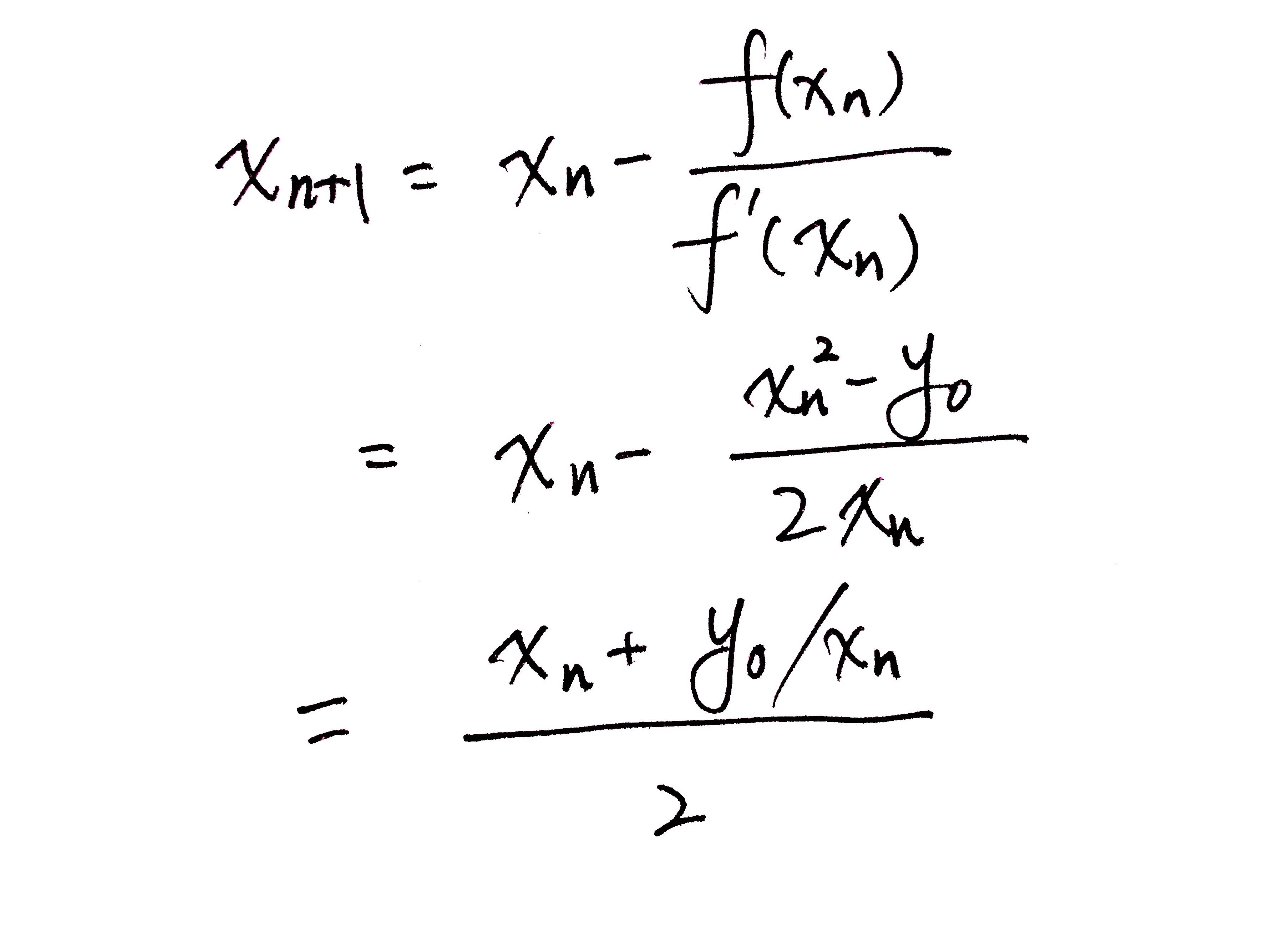
Origin of Quake3's Fast InvSqrt()
class Solution {
public int mySqrt(int x) {
long r = x;
while (r * r > x) {
r = (r + x / r) / 2;
}
return (int)r;
}
}