排序算法
比较类排序: 通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序: 不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时 间下界,以线性时间运行,因此也称为线性时间非比较类排序。
排序算法
比较类排序
交换排序
冒泡排序
快速排序
插入排序
简单插入排序
希尔排序
选择排序
简单选择排序
堆排序
归并排序
二路归并排序
多路归并排序
非比较排序
计数排序
桶排序
基数排序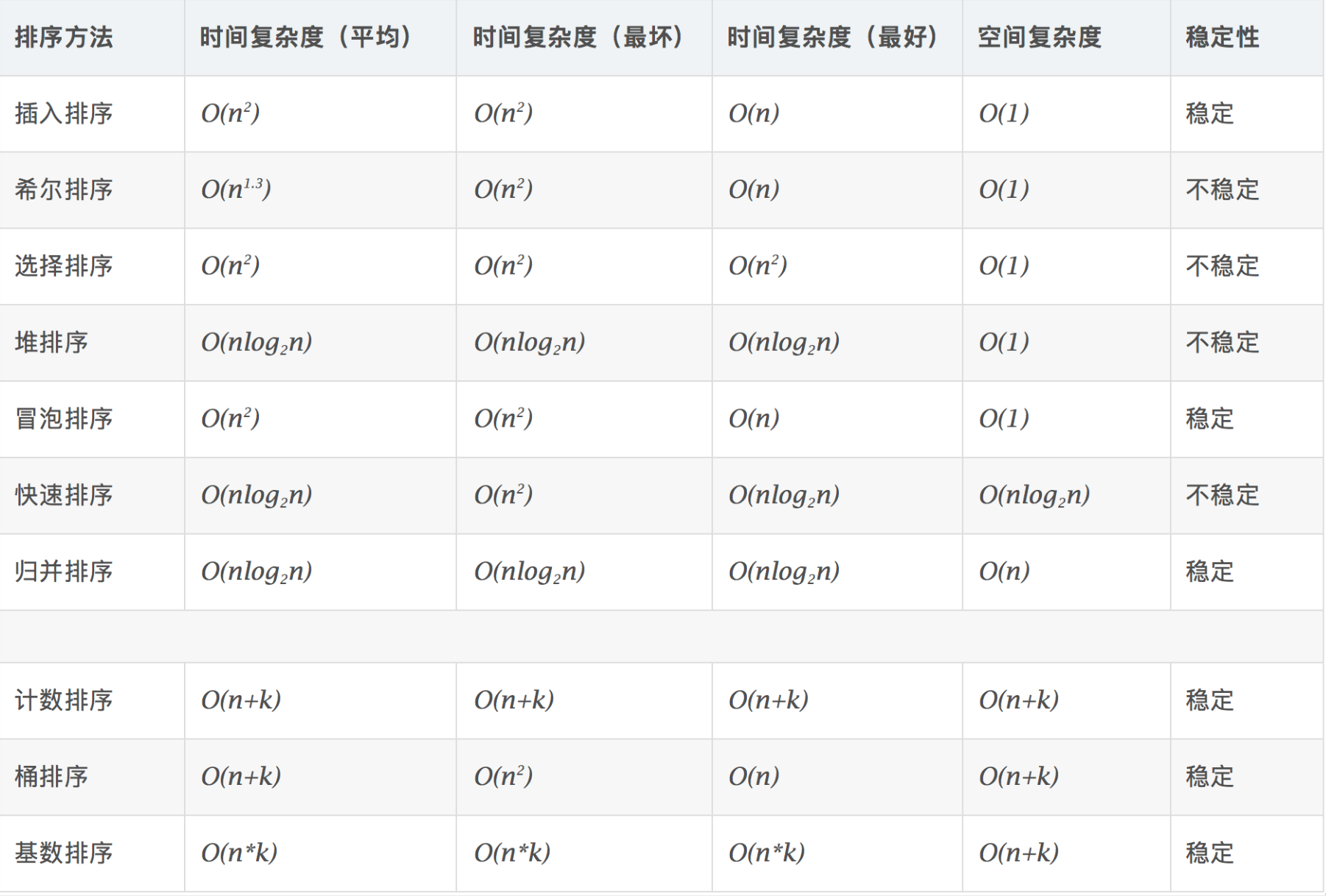
初级排序 - O(n^2)
- 选择排序(Selection Sort) 每次找最小值,然后放到待排序数组的起始位置。
- 插入排序(Insertion Sort) 从前到后逐步构建有序序列; 对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
- 冒泡排序(Bubble Sort) 嵌套循环,每次查看相邻的元素如果逆序,则交换。
高级排序 - O(N*LogN)
快速排序(Quick Sort)
数组取标杆 pivot,将小元素放 pivot左边,大元素放右侧,然后依次 对左边和右边的子数组继续快排;以达到整个序列有序。
归并排序(Merge Sort)— 分治
- 把长度为n的输入序列分成两个长度为n/2的子序列; 2. 对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
归并 和 快排 具有相似性,但步骤顺序相反 归并: 先排序左右子数组,然后合并两个有序子数组 快排: 先调配出左右子数组,然后对于左右子数组进行排序
堆排序(Heap Sort) — 堆插入 O(logN),取最大/小值 O(1)
- 数组元素依次建立小顶堆
- 依次取堆顶元素,并删除
特殊排序 - O(n)
- 计数排序(Counting Sort) 计数排序要求输入的数据必须是有确定范围的整数。将输入的数据值转化为键存 储在额外开辟的数组空间中;然后依次把计数大于 1 的填充回原数组
- 桶排序(Bucket Sort) 桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有 限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式 继续使用桶排序进行排)。
- 基数排序(Radix Sort) 基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类 推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按 高优先级排序。
代码模版
冒泡排序
public void bubbleSort(int[] a) {
if (a.length <= 0) return;
for (int i = 0; i < a.length; i++) {
boolean flag = false;
for (int j = 0; j < a.length-i-1; j++) {
if(a[j] > a[j+1]) {
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
}
if (!flag) break; // 没有数据交换,提前退出
}
}
插入排序
public void insertionSort(int[] a) {
int n = a.length;
if(n <= 1) return;
for (int i = 1; i < n; i++) {
int value = a[i];
int j = i-1;
for (; j >= 0 ; j--) {
if(a[j] > value) {
a[j+1] = a[j];
} else {
break;
}
}
a[j+1] = value;
}
}
选择排序
public void selectionSort(int[] a){
int n = a.length;
if (n <= 0) return;
for (int i = 0; i < n; i++) {
int minIndex = i;
for (int j = i; j < n; j++) {
if(a[j] < a[minIndex]) {
minIndex = j;
}
}
if(minIndex != i) {
int tmp = a[i];
a[i] = a[minIndex];
a[minIndex] = tmp;
}
}
}
归并排序
public void mergeSort(int[] a, int low, int high) {
if (low >= high) return;
int mid = (low + high) >>> 1;
mergeSort(a, low, mid);
mergeSort(a, mid+1, high);
merge(a, low, mid, high);
}
public void merge(int[] a, int low, int mid, int high) {
int i = low;
int j = mid + 1;
int k = 0;
int[] tmp = new int[high-low+1];
while(i <= mid && j <= high) {
if(a[i] <= a[j]) {
tmp[k++] = a[i++];
} else {
tmp[k++] = a[j++];
}
}
int start = i;
int end = mid;
if (j <= high) {
start = j;
end = high;
}
while (start <= end) {
tmp[k++] = a[start++];
}
for (int l = 0; l < high-low+1; l++) {
a[low+l] = tmp[l];
}
}
// 归并排序代码-Java
public static void mergeSort(int[] array, int left, int right) {
if (right <= left) return;
int mid = (left + right) >>> 1; // (left + right) / 2
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
merge(array, left, mid, right);
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1]; // 中间数组
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
for (int p = 0; p < temp.length; p++) {
arr[left + p] = temp[p];
}
// 也可以用 System.arraycopy(a, start1, b, start2, length) }
}
快排
// 快排代码-Java
public static void quickSort(int[] array, int begin, int end) {
if (end <= begin) return;
int pivot = partition(array, begin, end);
quickSort(array, begin, pivot - 1);
quickSort(array, pivot + 1, end);
}
static int partition(int[] a, int begin, int end) { // pivot: 标杆位置,counter: 小于pivot的元素的个数
int pivot = end, counter = begin;
for (int i = begin; i < end; i++) {
if (a[i] < a[pivot]) {
int temp = a[counter];
a[counter] = a[i];
a[i] = temp;
counter++;
}
}
int temp = a[pivot];
a[pivot] = a[counter];
a[counter] = temp;
return counter;
}
堆排序
void heap_sort(int a[], int len) {
priority_queue<int, vector<int>, greater<int>> q;
for (int i = 0; i < len; i++) {
q.push(a[i]);
}
for (int i = 0; i < len; i++) {
a[i] = q.pop();
}
}
static void heapify(int[] array, int length, int i) {
int left = 2 * i + 1, right = 2 * i + 2;
int largest = i;
if (left < length && array[left] > array[largest]) {
largest = leftChild;
}
if (right < length && array[right] > array[largest]) {
largest = right;
}
if (largest != i) {
int temp = array[i];
array[i] = array[largest];
array[largest] = temp;
heapify(array, length, largest);
}
}
public static void heapSort(int[] array) {
if (array.length == 0) return;
int length = array.length;
for (int i = length / 2 - 1; i >= 0; i -)
heapify(array, length, i);
for (int i = length - 1; i >= 0; i--) {
int temp = array[0];
array[0] = array[i];
array[i] = temp;
heapify(array, i, 0);
}
}
参考链接
十大经典排序算法
十大经典排序算法最强总结(含JAVA代码实现)
9 种经典排序算法可视化动画
6 分钟看完 15 种排序算法动画展示